34. Convolutional Layers in PyTorch
Convolutional Layers in PyTorch
To create a convolutional layer in PyTorch, you must first import the necessary module:
import torch.nn as nnThen, there is a two part process to defining a convolutional layer and defining the feedforward behavior of a model (how an input moves through the layers of a network). First, you must define a Model class and fill in two functions.
init
You can define a convolutional layer in the
__init__
function of by using the following format:
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0)forward
Then, you refer to that layer in the forward function! Here, I am passing in an input image
x
and applying a ReLU function to the output of this layer.
x = F.relu(self.conv1(x))Arguments
You must pass the following arguments:
-
in_channels- The number of inputs (in depth), 3 for an RGB image, for example. -
out_channels- The number of output channels, i.e. the number of filtered "images" a convolutional layer is made of or the number of unique, convolutional kernels that will be applied to an input. -
kernel_size- Number specifying both the height and width of the (square) convolutional kernel.
There are some additional, optional arguments that you might like to tune:
-
stride- The stride of the convolution. If you don't specify anything,strideis set to1. -
padding- The border of 0's around an input array. If you don't specify anything,paddingis set to0.
NOTE
: It is possible to represent both
kernel_size
and
stride
as either a number or a tuple.
There are many other tunable arguments that you can set to change the behavior of your convolutional layers. To read more about these, we recommend perusing the official documentation .
Pooling Layers
Pooling layers take in a kernel_size and a stride. Typically the same value as is the down-sampling factor. For example, the following code will down-sample an input's x-y dimensions, by a factor of 2:
self.pool = nn.MaxPool2d(2,2)forward
Here, we see that poling layer being applied in the forward function.
x = F.relu(self.conv1(x))
x = self.pool(x)Convolutional Example #1
Say I'm constructing a CNN, and my input layer accepts grayscale images that are 200 by 200 pixels (corresponding to a 3D array with height 200, width 200, and depth 1). Then, say I'd like the next layer to be a convolutional layer with 16 filters, each filter having a width and height of 2. When performing the convolution, I'd like the filter to jump two pixels at a time. I also don't want the filter to extend outside of the image boundaries; in other words, I don't want to pad the image with zeros. Then, to construct this convolutional layer, I would use the following line of code:
self.conv1 = nn.Conv2d(1, 16, 2, stride=2)Convolutional Example #2
Say I'd like the next layer in my CNN to be a convolutional layer that takes the layer constructed in Example 1 as input. Say I'd like my new layer to have 32 filters, each with a height and width of 3. When performing the convolution, I'd like the filter to jump 1 pixel at a time. I want this layer to have the same width and height as the input layer, and so I will pad accordingly. Then, to construct this convolutional layer, I would use the following line of code:
self.conv2 = nn.Conv2d(16, 32, 3, padding=1)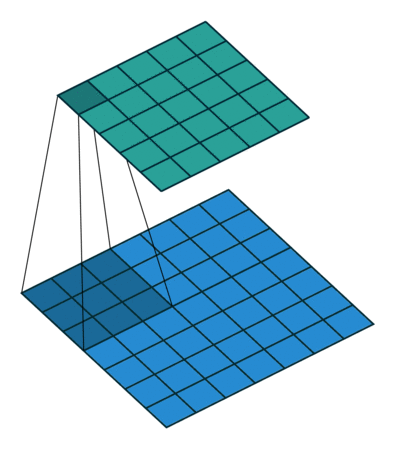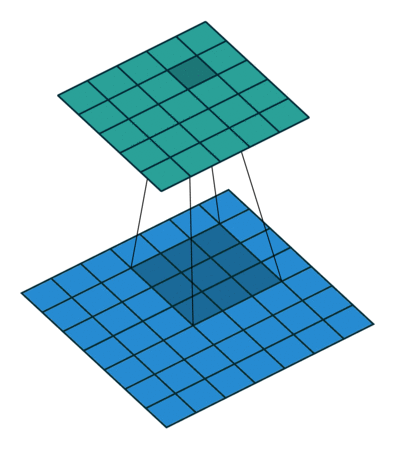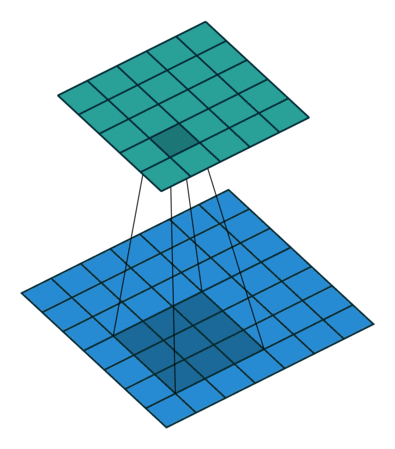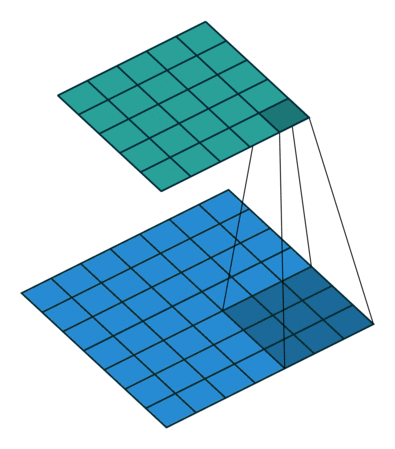
Convolution with 3x3 window and stride 1
Image source: http://iamaaditya.github.io/2016/03/one-by-one-convolution/
Sequential Models
We can also create a CNN in PyTorch by using a
Sequential
wrapper in the
__init__
function. Sequential allows us to stack different types of layers, specifying activation functions in between!
def __init__(self):
super(ModelName, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(1, 16, 2, stride=2),
nn.MaxPool2d(2, 2),
nn.ReLU(True),
nn.Conv2d(16, 32, 3, padding=1),
nn.MaxPool2d(2, 2),
nn.ReLU(True)
)Formula: Number of Parameters in a Convolutional Layer
The number of parameters in a convolutional layer depends on the supplied values of
filters/out_channels
,
kernel_size
, and
input_shape
. Let's define a few variables:
-
K- the number of filters in the convolutional layer -
F- the height and width of the convolutional filters -
D_in- the depth of the previous layer
Notice that
K
=
out_channels
, and
F
=
kernel_size
. Likewise,
D_in
is the last value in the
input_shape
tuple, typically 1 or 3 (RGB and grayscale, respectively).
Since there are
F*F*D_in
weights per filter, and the convolutional layer is composed of
K
filters, the total number of weights in the convolutional layer is
K*F*F*D_in
. Since there is one bias term per filter, the convolutional layer has
K
biases. Thus, the
_ number of parameters_
in the convolutional layer is given by
K*F*F*D_in + K
.
Formula: Shape of a Convolutional Layer
The shape of a convolutional layer depends on the supplied values of
kernel_size
,
input_shape
,
padding
, and
stride
. Let's define a few variables:
-
K- the number of filters in the convolutional layer -
F- the height and width of the convolutional filters -
S- the stride of the convolution -
P- the padding -
W_in- the width/height (square) of the previous layer
Notice that
K
=
out_channels
,
F
=
kernel_size
, and
S
=
stride
. Likewise,
W_in
is the first and second value of the
input_shape
tuple.
The
depth
of the convolutional layer will always equal the number of filters
K
.
The spatial dimensions of a convolutional layer can be calculated as:
(W_in−F+2P)/S+1
Flattening
Part of completing a CNN architecture, is to flatten the eventual output of a series of convolutional and pooling layers, so that all parameters can be seen (as a vector) by a linear classification layer. At this step, it is imperative that you know exactly how many parameters are output by a layer.
For the following quiz questions, consider an input image that is
130x130 (x, y) and 3
in depth (RGB). Say, this image goes through the following layers in order:
nn.Conv2d(3, 10, 3)
nn.MaxPool2d(4, 4)
nn.Conv2d(10, 20, 5, padding=2)
nn.MaxPool2d(2, 2)